Measuring Forecast Accuracy with Linear Programming
Using optimization of a battery to measure forecast accuracy.
This post introduces a methodology to measure the accuracy of an electricity price forecast using linear programming.
Predictive Accuracy vs. Business Value
The ideal forecast quality measurement directly aligns with a key business metric. Models are not often able to be trained in this way - often models are trained using error measures that will look familiar to anyone who does gradient based optimization, such as mean squared error.
This post uses a linear programming to measure forecast quality in terms of a key business metric - cost.
A battery operating in price arbitrage is optimized using actual prices and forecast prices.
The forecast error can then be quantified by how much money dispatching the battery using the forecast leaves on the table versus dispatching with perfect foresight of prices.
Data
This work uses energy-py-linear for the battery linear program - you can find the code & data in examples/forecast-accuracy.py - the full source code is also available at the bottom of this post.
$ pip install energypylinear
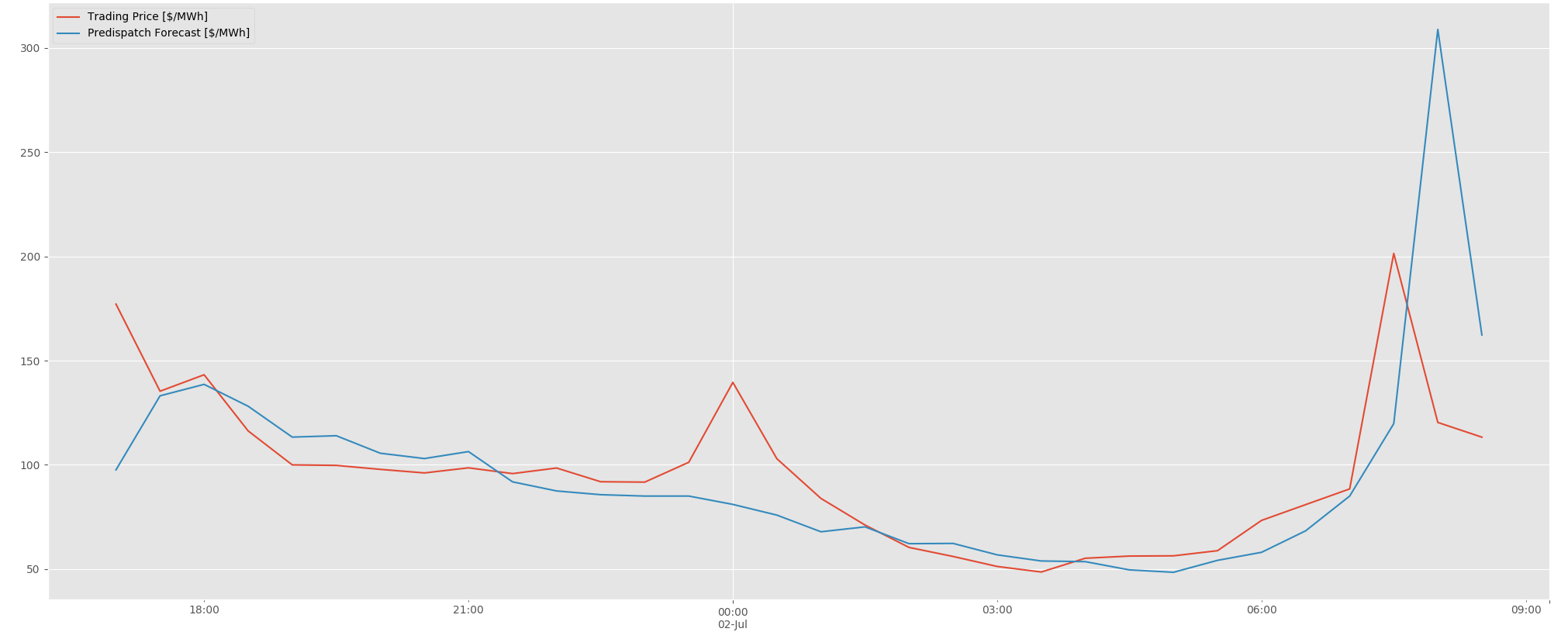
The dataset used is a single sample of the South Australian trading price and the AEMO predispatch price forecast.
Both the price and forecast are supplied by AEMO for the National Electricity Market (NEM) in Australia.
A simple plot of the price and forecast is show below in Figure 1:
Method
First we create an instance of the Battery class. We use a large capacity battery so that the battery will chase after all possible arbitrage opportunities with a roundtrip efficiency of 100%.
import energypylinear as epl
asset = epl.battery.Battery(power_mw=2, capacity_mwh=4, efficiency=0.9)
We then dispatch the battery using perfect foresight of prices:
actuals = asset.optimize(
electricity_prices=data['Trading Price [$/MWh]'],
freq_mins=30,
)
Next we dispatch using the forecast:
forecasts = asset.optimize(
electricity_prices=data['Predispatch Forecast [$/MWh]'],
freq_mins=30,
)
We can then create epl.Account objects to represent the financials for these two simulations.
The trick is using the actuals interval data with the forecast simulation in forecast_account - this evaluates the economics with actual prices but dispatch optimized for forecasts:
# calculate the variance between accounts
actual_account = epl.get_accounts(actuals.interval_data, actuals.simulation)
forecast_account = epl.get_accounts(actuals.interval_data, forecasts.simulation)
variance = actual_account - forecast_account
print(f"\nforecast error: $ {-1 * variance.cost:2.2f} pct: {100 * variance.cost / actual_account.cost:2.1f} %")
forecast error: $ 92.97 pct: 28.5 %
Discussion
Extend to Different Domains
The method above is specific to using batteries for wholesale price arbitrage.
The idea of using variance between two optimization runs with different inputs can be extended to many business problems.
If there is any error in the optimization (say to a local minima) then the final quality measurement combines the error from both forecasting and from the optimization that used the forecast.
A large capacity battery operating in price arbitrage does somewhat resemble arbitrage of stocks, so the error measurement might be useful for comparing forecasts. It’s less clear how useful this model would be for a temperature prediction.
Negative Value
A challenge with using this measurement of forecast error is what happens when the net benefit of dispatching the battery to a forecast - i.e. when the forecast quality is so bad that using it ends up losing money. Unlike other error measures such as mean squared error it’s not appropriate to simply take the absolute.
Full Example
import io
import pandas as pd
import energypylinear as epl
if __name__ == "__main__":
# price and forecast csv data
data = """
Timestamp,Trading Price [$/MWh],Predispatch Forecast [$/MWh]
2018-07-01 17:00:00,177.11,97.58039000000001
2018-07-01 17:30:00,135.31,133.10307
2018-07-01 18:00:00,143.21,138.59978999999998
2018-07-01 18:30:00,116.25,128.09559
2018-07-01 19:00:00,99.97,113.29413000000001
2018-07-01 19:30:00,99.71,113.95063
2018-07-01 20:00:00,97.81,105.5491
2018-07-01 20:30:00,96.1,102.99768
2018-07-01 21:00:00,98.55,106.34366000000001
2018-07-01 21:30:00,95.78,91.82700000000001
2018-07-01 22:00:00,98.46,87.45
2018-07-01 22:30:00,91.88,85.65775
2018-07-01 23:00:00,91.69,85.0
2018-07-01 23:30:00,101.2,85.0
2018-07-02 00:00:00,139.55,80.99999
2018-07-02 00:30:00,102.9,75.85762
2018-07-02 01:00:00,83.86,67.86758
2018-07-02 01:30:00,71.1,70.21946
2018-07-02 02:00:00,60.35,62.151
2018-07-02 02:30:00,56.01,62.271919999999994
2018-07-02 03:00:00,51.22,56.79063000000001
2018-07-02 03:30:00,48.55,53.8532
2018-07-02 04:00:00,55.17,53.52591999999999
2018-07-02 04:30:00,56.21,49.57504
2018-07-02 05:00:00,56.32,48.42244
2018-07-02 05:30:00,58.79,54.15495
2018-07-02 06:00:00,73.32,58.01054
2018-07-02 06:30:00,80.89,68.31508000000001
2018-07-02 07:00:00,88.43,85.0
2018-07-02 07:30:00,201.43,119.73926999999999
2018-07-02 08:00:00,120.33,308.88984
2018-07-02 08:30:00,113.26,162.32117
"""
data = pd.read_csv(io.StringIO(data))
# battery model
asset = epl.battery.Battery(power_mw=2, capacity_mwh=4, efficiency=0.9)
# optimize for actuals
actuals = asset.optimize(
electricity_prices=data["Trading Price [$/MWh]"],
freq_mins=30,
)
# optimize for forecasts
forecasts = asset.optimize(
electricity_prices=data["Predispatch Forecast [$/MWh]"],
freq_mins=30,
)
# calculate the variance between accounts
actual_account = epl.get_accounts(actuals.interval_data, actuals.simulation)
forecast_account = epl.get_accounts(actuals.interval_data, forecasts.simulation)
variance = actual_account - forecast_account
print(
f"\nforecast error: $ {-1 * variance.cost:2.2f} pct: {100 * variance.cost / actual_account.cost:2.1f} %"
)
"""
forecast error: $ 92.97 pct: 28.5 %
"""
Summary
This post introduces a method for measuring forecast accuracy using linear optimization of electric battery storage, by looking at the difference between two optimization runs given actual and forecast prices as input.
Thanks for reading!