Gas Turbines and Ambient Temperature

Gas turbine power output increases when it is cold, and decreases when it is hot. Being able to explain why is a great conversation starter at parties. It’s also something the energy engineer must account for when modelling gas turbines.

To explain the relationship we need to link together a few insights

• A gas turbine is a fixed volume machine.  You can only squeeze a fixed volume of air through the compressor and turbine.
• The density of air increases when it is cold.  Colder air means more mass of air in the same amount of volume.
• The amount of power generated in the turbine increases with a higher mass of air flowing through the turbine.

Colder air means we get a higher mass flow rate of air through the gas turbine. This higher mass flow through the turbine means more power generated.

When it gets hot the opposite effect occurs.  Power output decreases due to less mass flowing through the turbine.

Ambient temperature also has an affect on the compressor.  Colder air improves compressor efficiency.  This means the compressor consumes less power, leading to more power supplied to the generator.

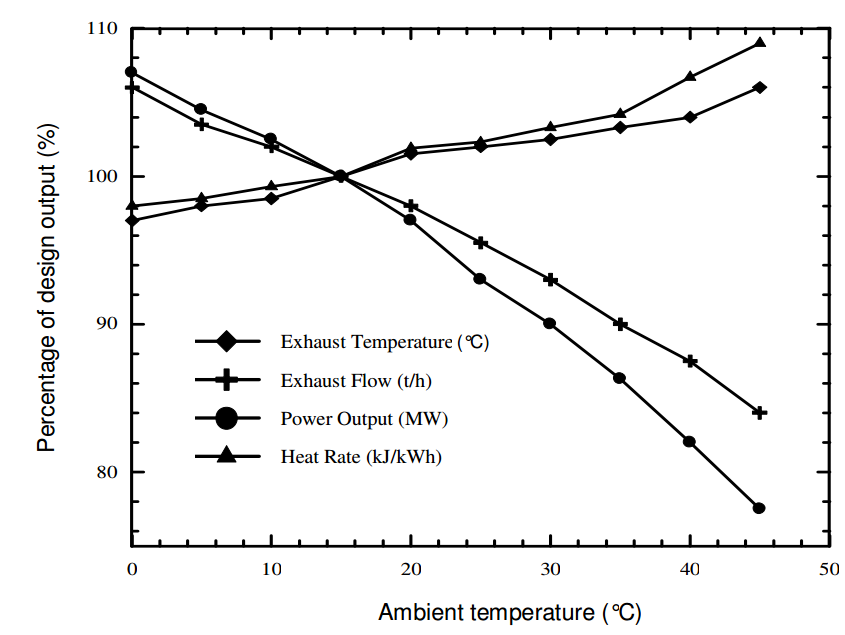
Figure 1 - Effect of ambient temperature on gas turbine performance. Rahman et. al (2011) - Thermodynamic performance analysis of gas-turbine power-plant

De Sa & Zubaidy (2011) proposed an empirical relationship for a 265 MW gas turbine. This gives us a rough rule of thumb of a 1% efficiency reduction and 5% reduction in output for every 10 °C change.

For every K rise in ambient temperature above ISO conditions the Gas Turbine loses 0.1% in terms of thermal efficiency and 1.47 MW of its Gross (useful) Power Output.

This relationship is a problem hot climates where peak demand will occur at the same time as reduced gas turbine output. It’s also a benefit in cold countries where peak often occurs when it’s very cold.

When an energy engineer models a gas turbine system she needs to be careful to account for this variation.  Most ideal is using a years worth of ambient temperature data on an hourly basis.

A simple linear regression between the variable (such as gas turbine output or efficiency) and ambient temperature will account for the variation for each hour.  Multiple linear regression can be used if both ambient temperature and gas turbine load are variable.

Thanks for reading!