Cross Entropy Method

This post introduces a parallelized implementation of the cross entropy method (CEM). CEM is often recommended as a first step before using a more complex method like reinforcement learning. The source code is available on github.

CEM optimizes parameters by:

• sampling parameters from a distribution
• evaluating parameters using total episode reward
• selecting the elite parameters
• refitting the sampling distribution using the elite parameters
• repeat

The sampling distribution is refit and sampled from using statistics (mean and standard deviation) from the elite population:

thetas = np.random.multivariate_normal(
	mean=means,
	cov=np.diag(np.array(stds**2) + extra_cov),
	size=batch_size
)

The advantages of CEM are:

• simple
• gradient free
• stable across random seeds
• easily parallelizable

The disadvantages are:

• only learn from entire episode trajectories (not individual actions)
• struggles with long horizon problems
• open loop planning only - can be suboptimal in stochastic environments

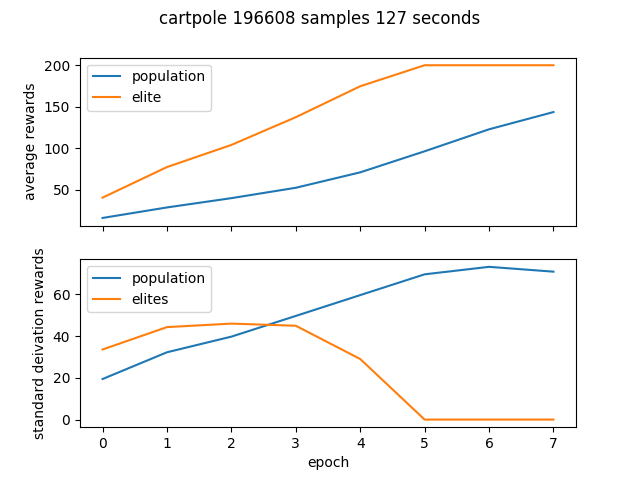
Performance

Results for the gym environments CartPole-v0 and Pendulum-v0. The standard deviation of the rewards shows how the elite population eventually becomes homogeneous.

Cartpole

$ python cem.py cartpole --num_process 6 --epochs 8 --batch_size 4096

Pendulum

$ python cem.py pendulum --num_process 6 --epochs 15 --batch_size 4096

Features of library

Parallelism over multiple process is achieved using Python’s multiprocessing library:

from multiprocessing import Pool
from functools import partial

#  need partial to send a fixed parameter into evaluate_theta()
with Pool(num_process) as p:
	rewards = p.map(partial(evaluate_theta, env_id=env_id), thetas)

Efficient sorting of parameters after evaluation in the environment is done using a binary heap:

import heapq

def get_elite_indicies(num_elite, rewards):
    return heapq.nlargest(num_elite, range(len(rewards)), rewards.take)

The source code for this library is on github here.

cem/cem.py

import argparse
from collections import defaultdict
import heapq
from multiprocessing import Pool
from functools import partial
import os
import time

import gym
import numpy as np

from envs import setup_env
from policies import setup_policy
from plotting import plot_history


def ensure_dir(file_path):
    directory = os.path.dirname(file_path)

    if not os.path.exists(directory):
        os.makedirs(directory)


def get_elite_indicies(num_elite, rewards):
    return heapq.nlargest(num_elite, range(len(rewards)), rewards.take)


def evaluate_theta(theta, env_id, monitor=False):
    env, _, _ = setup_env(env_id)

    if monitor:
        env = gym.wrappers.Monitor(env, env_id, force=False)

    policy = setup_policy(env, theta)

    done = False
    observation = env.reset()
    rewards = []

    while not done:

        action = policy.act(observation)
        next_observation, reward, done, info = env.step(action)

        rewards.append(reward)
        observation = next_observation

    return sum(rewards)


def run_cem(
        env_id,

        epochs=10,
        batch_size=4096,
        elite_frac=0.2,

        extra_std=2.0,
        extra_decay_time=10,

        num_process=4
):
    ensure_dir('./{}/'.format(env_id))

    start = time.time()
    num_episodes = epochs * num_process * batch_size
    print('expt of {} total episodes'.format(num_episodes))

    num_elite = int(batch_size * elite_frac)
    history = defaultdict(list)

    env, obs_shape, act_shape = setup_env(env_id)
    theta_dim = (obs_shape + 1) * act_shape
    means = np.random.uniform(size=theta_dim)
    stds = np.ones(theta_dim)

    for epoch in range(epochs):

        extra_cov = max(1.0 - epoch / extra_decay_time, 0) * extra_std**2

        thetas = np.random.multivariate_normal(
            mean=means,
            cov=np.diag(np.array(stds**2) + extra_cov),
            size=batch_size
        )

        with Pool(num_process) as p:
            rewards = p.map(partial(evaluate_theta, env_id=env_id), thetas)

        rewards = np.array(rewards)

        indicies = get_elite_indicies(num_elite, rewards)
        elites = thetas[indicies]

        means = elites.mean(axis=0)
        stds = elites.std(axis=0)

        history['epoch'].append(epoch)
        history['avg_rew'].append(np.mean(rewards))
        history['std_rew'].append(np.std(rewards))
        history['avg_elites'].append(np.mean(rewards[indicies]))
        history['std_elites'].append(np.std(rewards[indicies]))

        print(
            'epoch {} - {:2.1f} {:2.1f} pop - {:2.1f} {:2.1f} elites'.format(
                epoch,
                history['avg_rew'][-1],
                history['std_rew'][-1],
                history['avg_elites'][-1],
                history['std_elites'][-1]
            )
        )

    end = time.time()
    expt_time = end - start
    print('expt took {:2.1f} seconds'.format(expt_time))

    plot_history(history, env_id, num_episodes, expt_time)
    num_optimal = 3
    print('epochs done - evaluating {} best thetas'.format(num_optimal))

    best_theta_rewards = [evaluate_theta(theta, env_id, monitor=True)
                          for theta in elites[:num_optimal]]
    print('best rewards - {} acoss {} samples'.format(best_theta_rewards, num_optimal))

Thanks for reading!