Explaining the fully connected, convolution, LSTM and attention deep learning layer architectures.
This post is about four fundamental neural network layer architectures - the building blocks that machine learning engineers use to construct deep learning models.
The four layers are the:
For each layer we will look at:
All code examples are built using tensorflow==2.2.0 using the Keras Functional API.
A key term in this article is inductive bias - a useful term to sound clever and impress your friends at parties.
Inductive bias is the hard-coding of assumptions into the structure of a learning algorithm.
These assumptions make the model more special purpose, less flexible but more useful. By hard coding in assumptions about the structure of the data & task, we can learn functions from data that we otherwise would not be able to.
A bit of bias is good - this is a common lesson in machine learning (bias can be traded off for variance). This also holds in reinforcement learning, where unbiased approximations of a high variance Monte Carlo return performs worse than bootstrapped temporal difference methods.
Examples of inductive bias in other machine learning methods include:
The fully connected layer is the most general purpose deep learning layer.
Also known as a dense or feed-forward layer, this layer imposes the least amount of structure of our layers.
It will be found in almost all neural networks - if only used to control the size & shape of the output layer. Many neural networks use fully connected layers as a way to add capacity to the network in specific places.
At the heart of the fully connected layer is the artificial neuron - the distant ancestor of McCulloch & Pitt’s Threshold Logic Unit of 1943.
The artificial neuron is inspired by the biological neurons in our brains - however an artificial neuron is a shallow approximation of the complexity of a biological neuron.
The artificial neuron composed of three sequential steps:
The output of the activation function is input to all neurons (also known as nodes or units) in the next layer.
This is where the fully connected layer gets it’s name from - each node is fully connected to the nodes in the layers before & after it.

For the first layer, the node gets it’s input from the data being fed into the network (each data point is connected to each node). For last layer, the output is the prediction of the network.

The intuition behind all the connections in a fully connected layer is to put no restriction on information flow. It’s the intuition of having no intuition.
The fully connected layer imposes no structure and makes no assumptions about the data or task the network will perform. A neural network built of fully connected layers can be thought of as a blank canvas - impose no structure and let the network figure everything out.
This lack of structure is what gives neural networks of fully connected layers (of sufficient depth & width) the ability to approximate any function - known as the Universal Approximation Theorem.
The ability to learn any function at first sounds attractive. Why do we need any other architecture if a fully connected layer can learn anything?
Being able to learn in theory does not mean we can learn in practice. Actually finding the correct weights, using the data and learning algorithms (such as backpropagation) we have available may be impractical and unreachable.
The solution to these practical challenges is to use less specialized layers - layers that have assumptions about the data & task they are expected to perform. This specialization is their inductive bias.
A fully connected layer is the most general deep learning architecture - it imposes no constraints on the connectivity of each layer.
Use it when your data has no structure that you can take advantage of - if your data is a flat array (common in tabular data problems), then a fully connected layer is a good choice. Most neural networks will have fully connected layers somewhere.
Fully connected layers are common in reinforcement learning when learning from a flat environment observation.
For example, a network with a single fully connected layer is used in the Trust Region Policy Optimization (TRPO) paper from 2015:
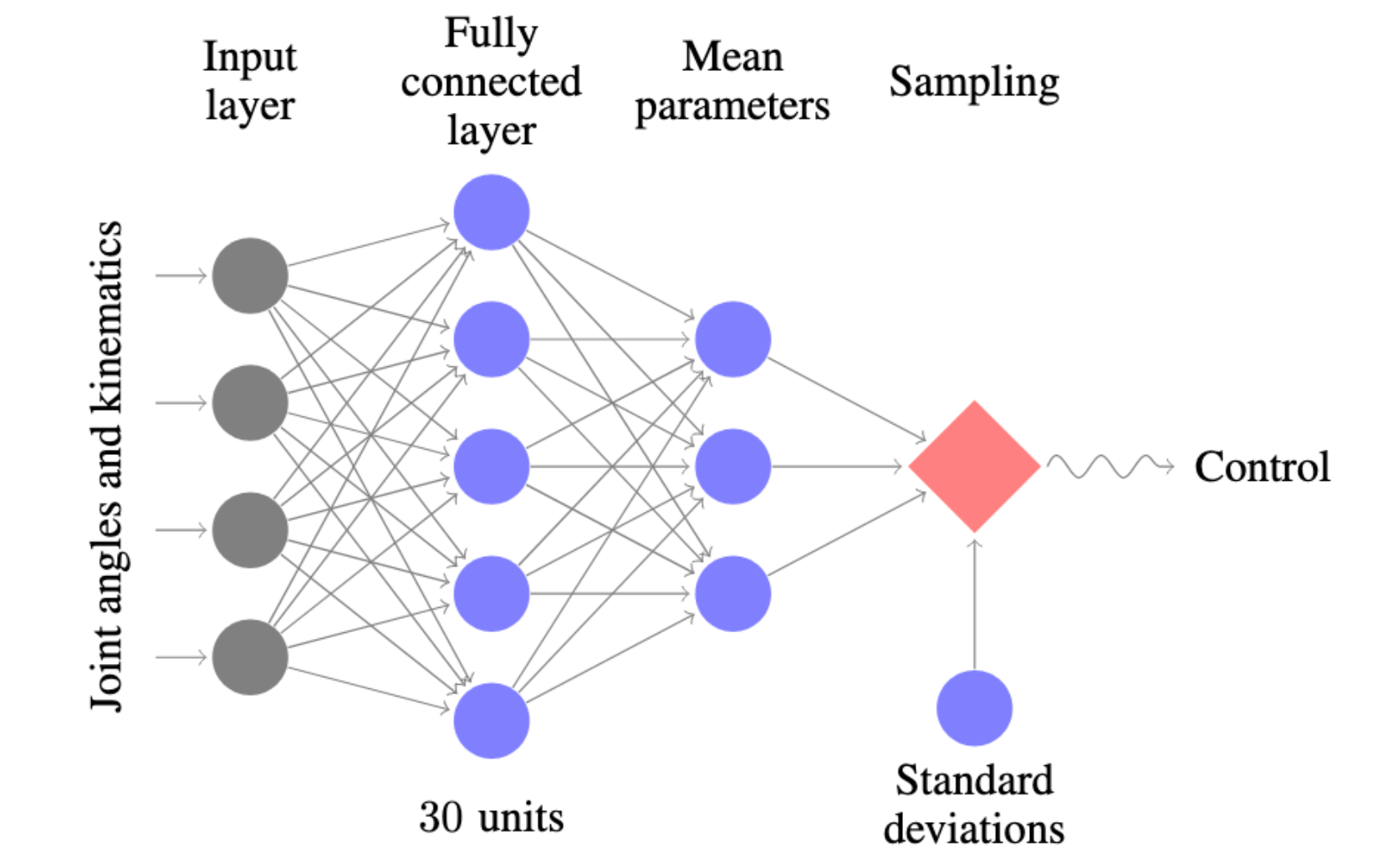
Fully connected layers are common as the penultimate & final layer as fully connected on convolutional neural networks performing classification. The number of units in the fully connected output layer will be equal to the number of classes, with a softmax activation function used to create a distribution over classes.
The two hyperparameters you’ll often set in a fully connected layer are the:
A fully connected layer is defined by a number of nodes (also known as units), each with an activation function. While you could have a layer with different activation functions on different nodes, most of the time each node in a layer has the same activation function.
For hidden layers, the most common choice of activation function is the rectified-linear unit (the ReLu). For the output layer, the correct activation function depends on what the network is predicting:
Below is an example of how to use a fully connected layer with the Keras functional API.
We are using input data shaped like an image, to show the flexibility of the fully connected layer - this requires us to use a Flatten layer later in the network:
import numpy as np
import tensorflow as tf
from tensorflow.keras import Input, Model
from tensorflow.keras.layers import Dense, Flatten
# the least random of all random seeds
np.random.seed(42)
tf.random.set_seed(42)
# dataset of 4 samples, 32x32 with 3 channels
x = np.random.rand(4, 32, 32, 3)
inp = Input(shape=x.shape[1:])
hidden = Dense(8, activation="relu")(inp)
flat = Flatten()(hidden)
out = Dense(2)(flat)
mdl = Model(inputs=inp, outputs=out)
mdl(x)
# <tf.Tensor: shape=(4, 2), dtype=float32, numpy=
# array([[ 0.23494382, -0.40392348],
# [ 0.10658629, -0.31808627],
# [ 0.42371386, -0.46299127],
# [ 0.34416917, -0.11493915]], dtype=float32)>If you had to pick one architecture as the most important in deep learning, it’s hard to look past convolution (see what I did there?).
The winner of the 2012 ImageNet competition, AlexNet, is seen by many as the start of modern deep learning. AlexNet was a deep convolutional neural network, trained on GPU to classify images.
Another landmark use of convolution is Le-Net-5 in 1998, a 7 layer convolutional neural network developed by Yann LeCun to classify handwritten digits.
The convolutional neural network is the original workhorse of the modern deep learning revolution - it can be used with text, audio, video and images.
Convolutional neural networks can be used to classify the contents of the image, recognize faces and create captions for images. They are also easy to parallelize on GPU - making them fast to train.
Convolution itself is a mathematical operation, commonly used in signal processing. The 2D convolutional layer is inspired by our own visual cortex.
The history of using convolution in artificial neural networks goes back decades to the neocognitron, an architecture introduced by Kunihiko Fukushima in 1980, inspired by the work of Hubel & Wiesel.
Work by the neurophysiologists Hubel & Wiesel in the 1950’s showed that individual neurons in the visual cortexes of mammals are activated by small regions of vision.

A good mental model for convolution is the process of sliding a filter over a signal, at each point checking to see how well the filter matches the signal.
This checking process is pattern recognition, and is the intuition behind convolution - looking for small, spatial patterns anywhere in a larger space. The convolution layer has inductive bias for recognizing local, spatial patterns.
A 2D convolutional layer is defined by the interaction between two components:
(height, width, color channels)(height, width)The intuition of convolution is looking for patterns in a larger space.
In a 2D convolutional layer, the patterns we are looking for are filters, and the larger space is an image.
A convolutional layer is defined by it’s filters. These filters are learnt - they are equivalent to the weights of a fully connected layer.
Filters in the first layers of a convolutional neural network detect simple features such as lines or edges. Deeper in the network, filters can detect more complex features that help the network perform it’s task.
To further understand how these filters work, let’s work with a small image and two filters. The basic operation in a convolutional neural network is to use these filters to detect patterns in the image, by performing element-wise multiplication and summing the result:

Reusing the same filters over the entire image allows features to be detected in any part of the image - a property known as translation invariance. This property is ideal for classification - you want to detect a cat no matter where it occurs in the image.
For larger images (which are often 32x32 or larger), this same basic operation is performed, with the filter being passed over the entire image. The output of this operation acts as feature detection, for the filters that the network has learnt, producing a 2D feature map.
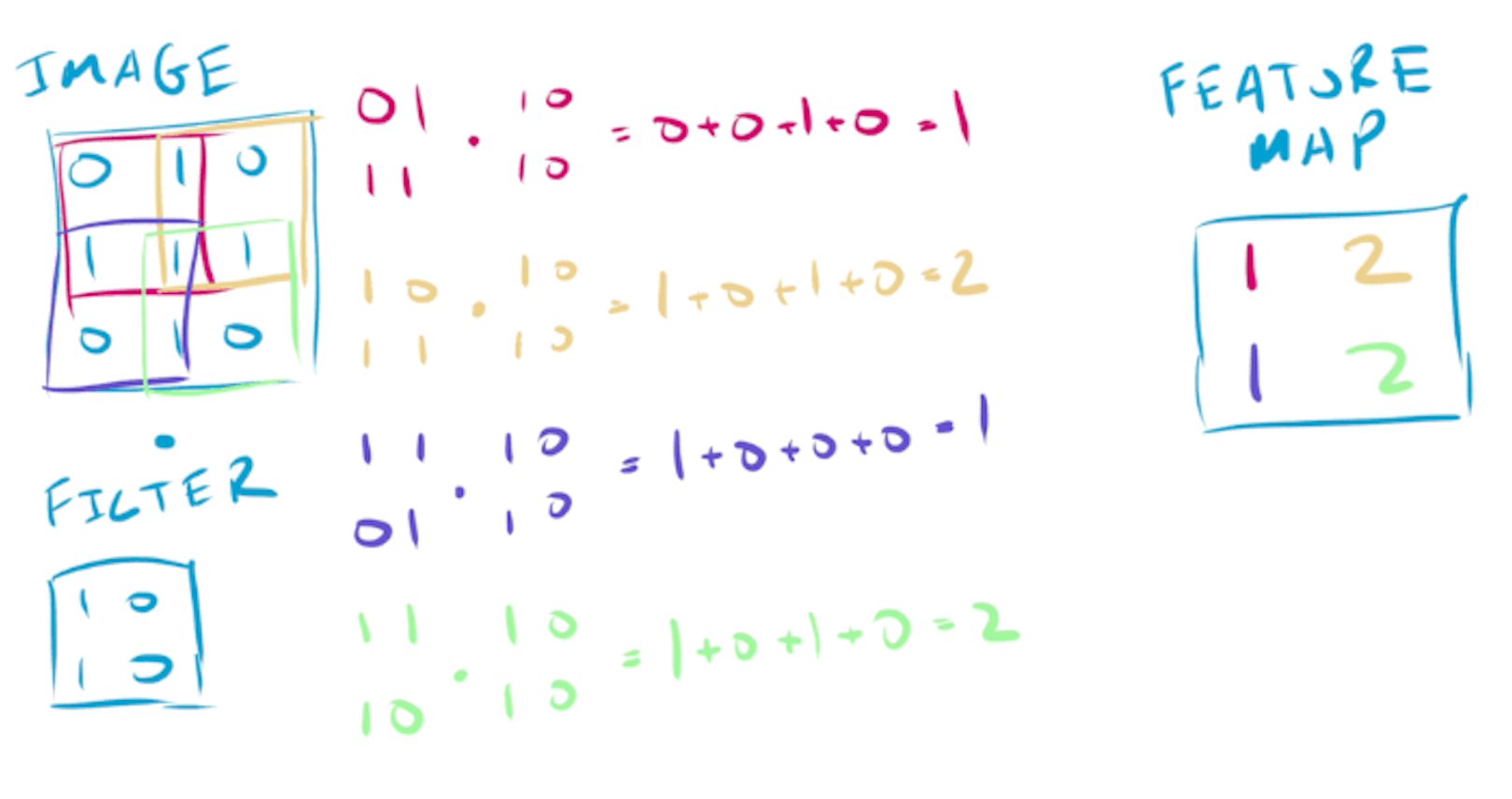
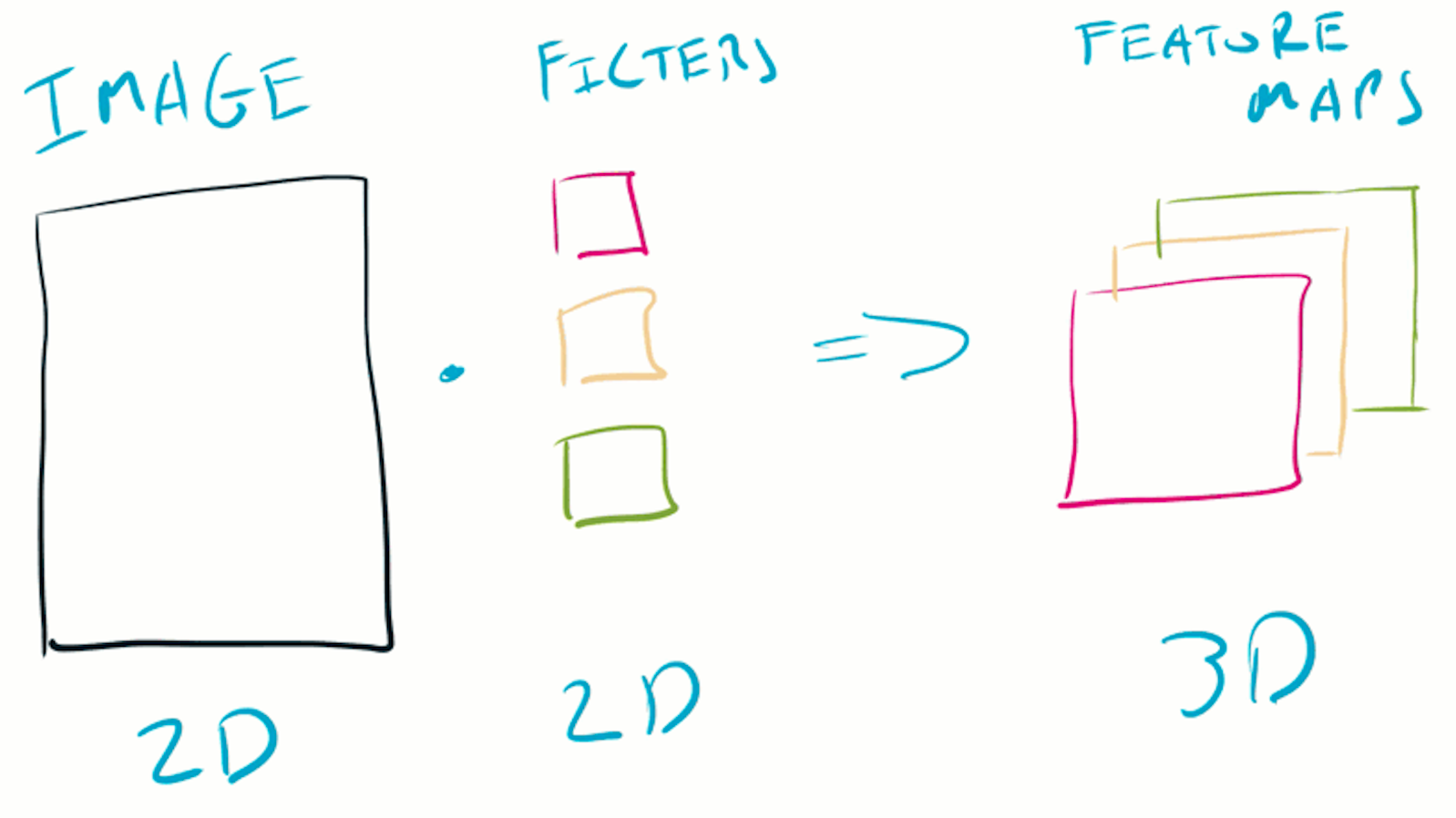
The feature maps produced by each filter are concatenated, resulting in a 3D volume (the length of the third dimension being the number of filters).
The next layer then performs convolution over this new volume, using a new set of learned filters.
Below is an example of how to use a 2D convolution layer with the Keras functional API:
Flatten layer before the dense layer, to flatten our volume produced by the 2D convolutional layerDense layer size of 8 - this controls how many classes our network can predictimport numpy as np
import tensorflow as tf
from tensorflow.keras import Input, Model
from tensorflow.keras.layers import Dense, Flatten, Conv2D
np.random.seed(42)
tf.random.set_seed(42)
# dataset of 4 images, 32x32 with 3 color channels
x = np.random.rand(4, 32, 32, 3)
inp = Input(shape=x.shape[1:])
conv = Conv2D(filters=8, kernel_size=(3, 3), activation="relu")(inp)
flat = Flatten()(conv)
feature_map = Dense(8, activation="relu")(flat)
out = Dense(2, activation="softmax")(flat)
mdl = Model(inputs=inp, outputs=out)
mdl(x)
# <tf.Tensor: shape=(4, 2), dtype=float32, numpy=
# array([[-0.39803684, -0.08939186],
# [-0.48165476, -0.28876644],
# [-0.32680377, -0.24380796],
# [-0.45394567, -0.28233868]], dtype=float32)>The important hyperparameters in a convolutional layer are:
(3, 3)Convolution works when your data has a spatial structure - for example, images have spatial structure in height & width. You can also get this structure from a 1D signal using techniques such as Fourier Transforms, and then perform convolution in the frequency domain.
If you are working with images, convolution is king. While there is work applying attention based models to computer vision, because of it’s similarity with our own visual cortex, it is likely that convolution will be relevant for many years to come.
An example of using convolution occurs in DeepMind’s 2015 DQN work. The agent learns to take decisions using pixels - making convolution a strong choice:

So what other kinds of structure can data have, other than spatial? Many types of data have a sequential structure - motivating our next two layer architectures.
The third of our layers is the LSTM, or Long Short-Term Memory layer. The LSTM is recurrent and processes data as a sequence.
Recurrence allows a network to experience the temporal structure of data, such as words in a sentence, or time of day.
A normal neural network receives a single input tensor $x$ and generates a single output tensor $y$. A recurrent architecture differs from a non-recurrent neural network in two ways:
The memory of a recurrent architecture is known as the hidden state $h$. What the network chooses to pass forward in the hidden state is learnt by the network.

Working with recurrent architectures requires being comfortable with the idea of a timestep dimension - knowing how to shape your data correctly is half the battle of working with recurrence.
Imagine we have input data $x$, that is a sequence of integers [0, 0] -> [2, 20] -> [4, 40]. If we were using a fully connected layer, we could present this data to the network as a flat array:
import numpy as np
x = np.zeros(10).astype(int)
x[0::2] = np.arange(0, 10, 2)
x[1::2] = np.arange(0, 100, 20)
x = x.reshape(1, -1)
print(x)
# array([[ 0, 0, 2, 20, 4, 40, 6, 60, 8, 80]])
print(x.shape)
# (1, 10)Although the sequence is obvious to us, it’s not obvious to a fully connected layer.
All a fully connected layer would see is a list of numbers - the sequential structure would need to be learnt by the network.
We can restructure our data $x$ to explicitly model this sequential structure, by adding a timestep dimension. The values in our data do not change - only the shape changes:
import numpy as np
x = np.vstack([np.arange(0, 10, 2), np.arange(0, 100, 20)]).T
x = x.reshape(1, 5, 2)
print(x)
# array([[[ 0, 0],
# [ 2, 20],
# [ 4, 40],
# [ 6, 60],
# [ 8, 80]]])
print(x.shape)
# (1, 5, 2)Our data $x$ is now structured with three dimensions - (batch, timesteps, features). A recurrent neural network will process the features one timestep at a time, experiencing the sequential structure of the data.
Now that we understand how to structure data to be used with a recurrent neural network, we can take a high-level look at details of how the LSTM layer works.
The LSTM was first introduced in 1997 and has formed the backbone of modern sequence based deep learning models, excelling on challenging tasks such as machine translation. For years the state of the art in machine translation was the seq2seq model, which is powered by the LSTM.
The LSTM is a specific type a recurrent neural network. The LSTM addresses a challenge that vanilla recurrent neural networks struggled with - the ability to think long term.
In a recurrent neural network all information passed to the next time step has to fit in a single channel, the hidden state $h$.
The LSTM addresses the long term memory problem by using two hidden states, known as the hidden state $h$ and the cell state $c$. Having two channels allows the LSTM to remember on both a long and short term.
Internally the LSTM makes use of three gates to control the flow of information:
One important architecture that uses LSTMs is seq2seq. The source sentence is fed through an encoder LSTM to generate a fixed length context vector. A second decoder LSTM takes this context vector and generates the target sentence.
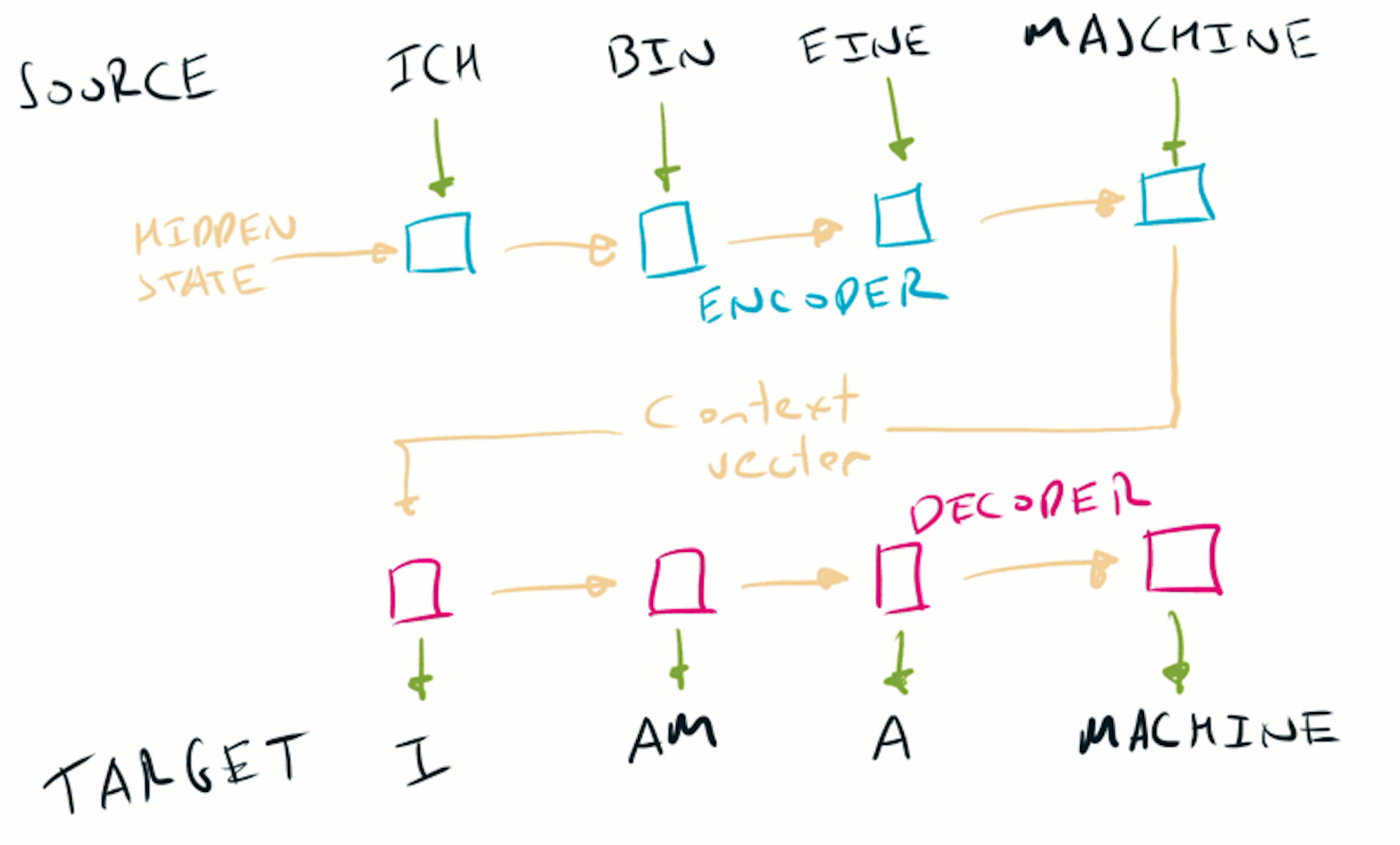
For a deeper look at the internal of the LSTM, take a look at the excellent Understanding LSTM Networks from colah’s blog.
A good intuitive model for the LSTM layer is to think about it like a database. The output, input and delete gates allow the LSTM to work like a database - matching the GET, POST & DELETE of a REST API, or the read-update-delete operations of a CRUD application.
The forget gate acts like a DELETE, allowing the LSTM to remove information that isn’t useful. The input gate acts like a POST, where the LSTM can choose information to remember. The output gate acts like a GET, where the LSTM chooses what to send back to a user request for information.
A recurrent neural network has has an inductive bias for processing data as a sequence, and for storing a memory. The LSTM adds on top of this bias for creating one long term and one short term memory channel.
Below is an example of how to use an LSTM layer with the Keras functional API:
import numpy as np
import tensorflow as tf
from tensorflow.keras import Input, Model
from tensorflow.keras.layers import Dense, LSTM, Flatten
np.random.seed(42)
tf.random.set_seed(42)
# dataset of 4 samples, 3 timesteps, 32 features
x = np.random.rand(4, 3, 32)
inp = Input(shape=x.shape[1:])
lstm = LSTM(8)(inp)
out = Dense(2)(lstm)
mdl = Model(inputs=inp, outputs=out)
mdl(x)
# <tf.Tensor: shape=(4, 2), dtype=float32, numpy=
# array([[-0.06428523, 0.3131591 ],
# [-0.04120642, 0.3528567 ],
# [-0.04273851, 0.37192333],
# [ 0.03797218, 0.33612275]], dtype=float32)>You’ll notice we only get one output for each of our four samples - where are the other two timesteps? To get these, we need to use return_sequences=True:
tf.random.set_seed(42)
inp = Input(shape=x.shape[1:])
lstm = LSTM(8, return_sequences=True)(inp)
out = Dense(2)(lstm)
mdl = Model(inputs=inp, outputs=out)
mdl(x)
# <tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
# array([[[-0.08234972, 0.12292314],
# [-0.05217044, 0.19100665],
# [-0.06428523, 0.3131591 ]],
#
# [[ 0.0381453 , 0.26402596],
# [ 0.04725918, 0.34620702],
# [-0.04120642, 0.3528567 ]],
#
# [[-0.21114576, 0.08922277],
# [-0.02972354, 0.24037611],
# [-0.04273851, 0.37192333]],
#
# [[-0.06888272, -0.01702049],
# [ 0.0117887 , 0.10608622],
# [ 0.03797218, 0.33612275]]], dtype=float32)>It’s also common to want to access the hidden states of the LSTM - this can be done using the argument return_state=True.
We now get back three tensors - the output of the network, the LSTM hidden state and the LSTM cell state. The shape of the hidden states is equal to the number of units in the LSTM:
tf.random.set_seed(42)
inp = Input(shape=x.shape[1:])
lstm, hstate, cstate = LSTM(8, return_sequences=False, return_state=True)(inp)
out = Dense(2)(lstm)
mdl = Model(inputs=inp, outputs=[out, hstate, cstate])
out, hstate, cstate = mdl(x)
print(hstate.shape)
# (4, 8)
print(cstate.shape)
# (4, 8)If you wanted to access the hidden states at each timestep, then you can combine these two and use both return_sequences=True and return_state=True.
For an LSTM layer, the main hyperparameter is the number of units. The number of units will determine the capacity of the layer and size of the hidden state.
While not a hyperparameter, it can be useful to include gradient clipping when working with LSTMs, to deal with exploding gradients that can occur from the backpropagation through time. It is also common to use lower learning rates to help manage gradients.
In 2025, the answer to this is never. If you have the type of data (sequential) that is suitable for an LSTM, you should look at using attention.
When working with sequence data, an LSTM (or it’s close cousin the GRU) used to be the best choice. One major downside of the LSTM is that they are slow to train as the error signal must be backpropagated through time. Backpropagating through an LSTM cannot be parallelized.
One useful feature of the LSTM is the learnt hidden state. This can be used by other models as a compressed representation of the future - such as in the 2017 World Models paper.
Attention is the youngest of our four layers.
Since it’s introduction in 2015, attention has revolutionized natural language processing. Attention powers some of the most breathtaking achievements in deep learning, such as the GPT-X series of language models.
First used in combination with the LSTM based seq2seq model, attention powers the Transformer - a neural network architecture that forms the backbone of modern language models.
Attention is a sequence model without recurrence - by avoiding the need to do backpropagation through time, attention can be parallelized on GPU, which means it’s fast to train.
Attention is a simple and powerful idea - when processing a sequence, we should choose what part of sequence to take information from. The intuition is simple - some parts of a sequence are more important that others.
Take the example of machine translation, to translate the German sentence Ich bin eine Machine into the English I am a machine.
When predicting the last word in the translation machine, all of our attention should be placed on the last word of the source sentence Machine. There is no point looking at earlier words in the source sequence when translating this token.
If we take a more complex example of translating the German Ich habe ein bisschen Deutsch gelernt into the English I have learnt a little German. When predicting the third token of our English sentence (learnt), attention should be placed on the last token of the German sentence (gelernt).
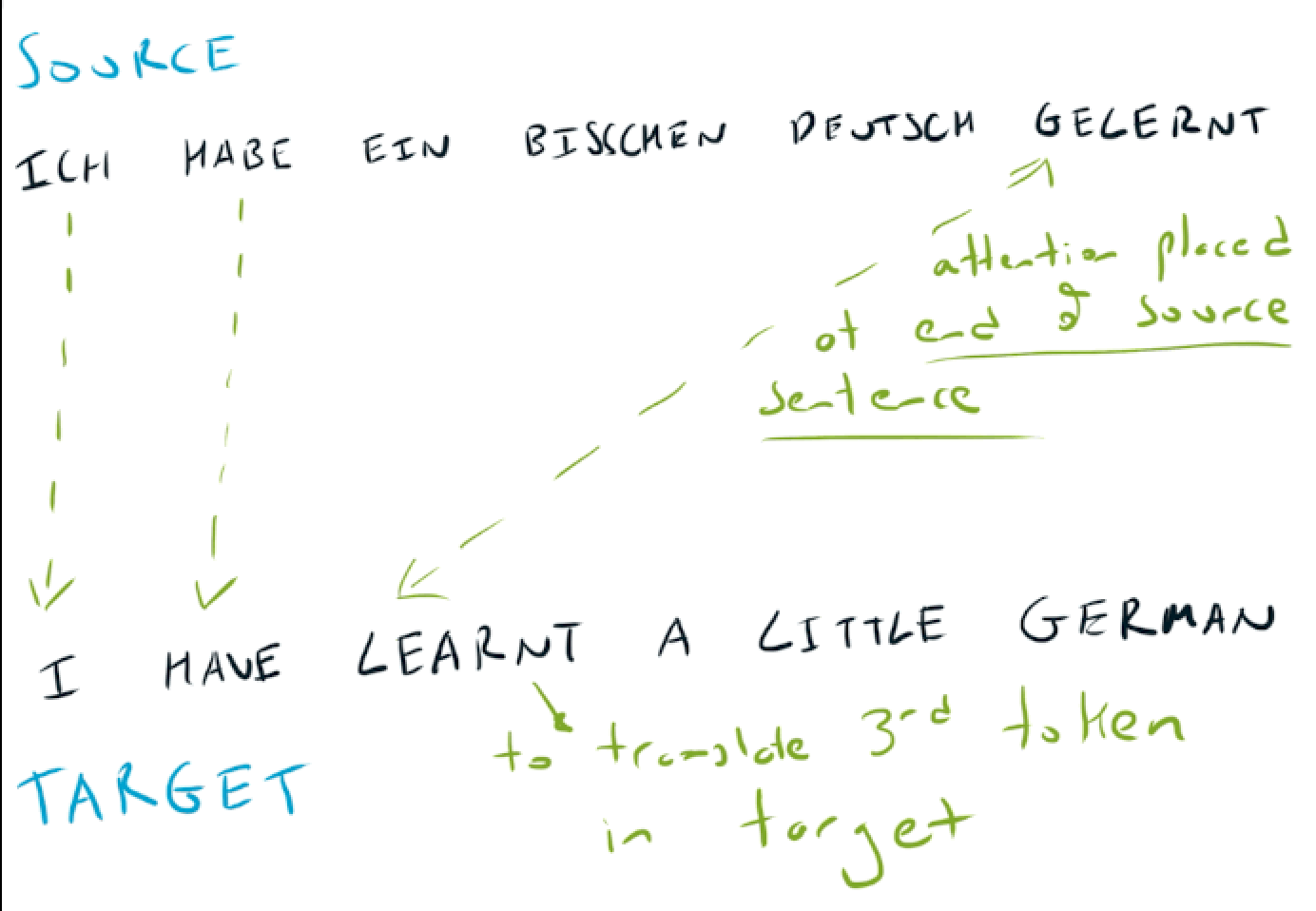
So what inductive bias does our attention layer give us? One inductive bias of attention is alignment based on similarity - the attention layer chooses where to look based on how similar things are.
Another inductive bias of attention is to limit & prioritize information flow. As we will see below, the use of a softmax forces an attention layer to make tradeoffs about information flow - more weight in one place means less in another.
There is no such restriction in a fully connected layer, where increasing one weight does not affect another. A fully connected layer can allow information to flow between all nodes in subsequent layers, and could in theory learn a similar pattern that an attention layer does. We know by now however that in theory does not mean it will occur in practice.
The attention layer receives three inputs:
The attention layer can be thought of as three mechanisms in sequence:
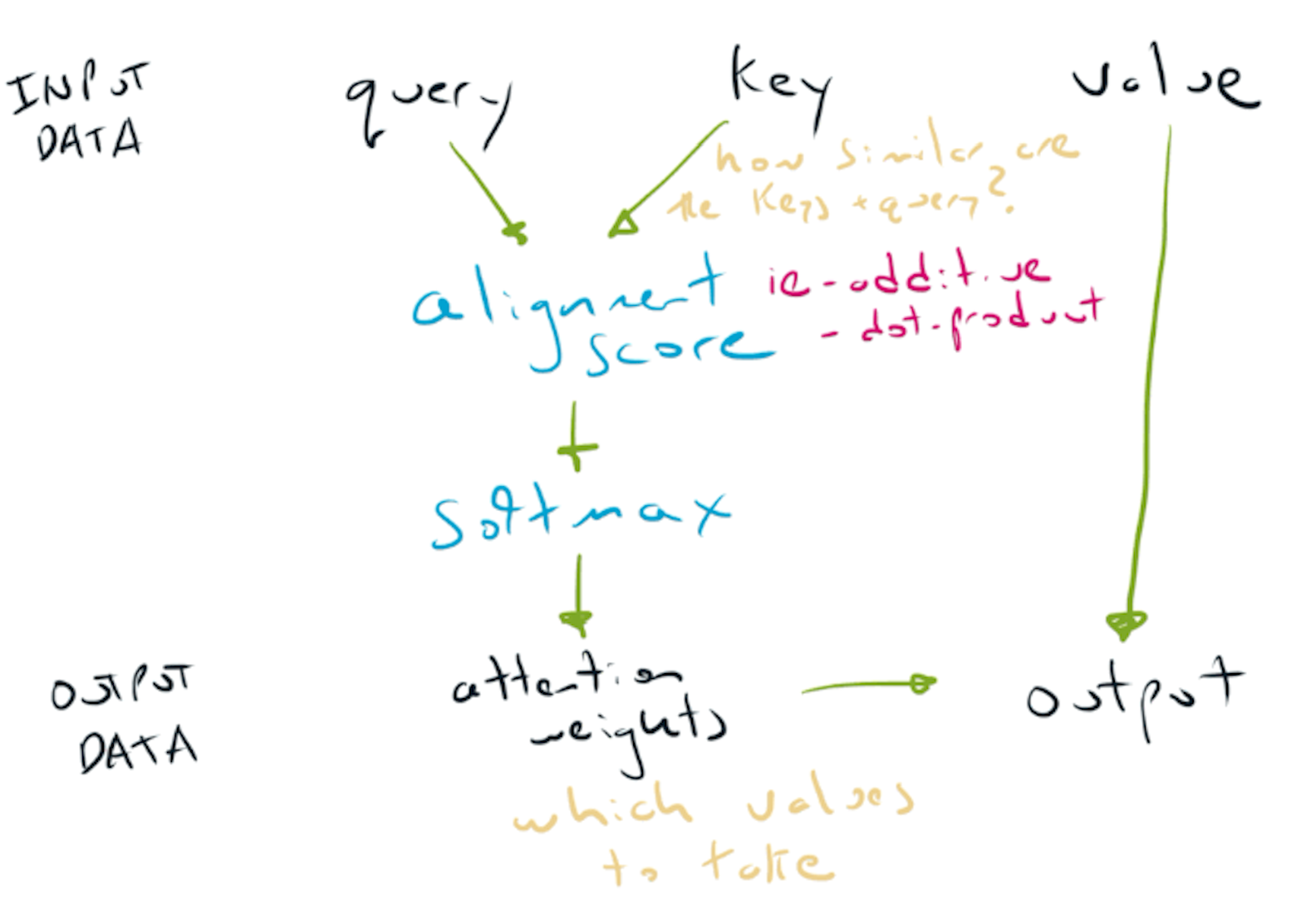
Different attention layers (such as Additive Attention or Dot-Product Attention) use different mechanisms in the alignment step. The softmax & key selection steps are common to all attention layers.
In the same way that understanding the time-step dimension is a key step in understanding recurrent neural networks, understanding what the query, key & value mean is foundational in attention.
A good analogy is with the Python dictionary. Let’s start with a simple example, where we:
dogdog or cat with values of 1 or 2 respectively2 based on this lookup of dogquery = "dog"
# keys = 'cat', 'dog', values = 1, 2
database = {"cat": 1, "dog": 2}
database[query]
# 2In the above example, we find an exact match for our query 'dog'. However, in a neural network, we are not working with strings - we are working with tensors. Our query, keys and values are all tensors:
query = [0, 0.9]
# keys = [0, 0], [0, 1] values = [0], [1]
database = {[0, 0]: [0], [0, 1]: [1]}Now we don’t have an exact match for our query - instead of using an exact match, we instead can calculate a similarity (i.e. an alignment) between our query and keys, and return the closest value:
database.similarity(query)
# [1]Small technicality - often the keys are set equal to the values. This simply means that the quantity we are doing the similarity comparison with is also the quantity we will place attention over.
By now we know that an attention layer involves three steps:
The second & third steps are common to all attention layers - the differences all occur in the first step - how the alignment on similarity is done.
We will briefly look at two popular mechanisms - Additive Attention and Dot-Product Attention. For a more detailed look at these mechanisms, have a look at the excellent Attention? Attention! by Lilian Wang.
This first use of attention (known as Bahdanau or Additive Attention) addressed one of the limitations of the seq2seq model - namely the use of a fixed length context vector.
As explained in the LSTM section, the basic process in a seq2seq model is to encode the source sentence into a fixed length context vector. The issue is with all of the information from the encoder must pass through the fixed length context vector. Information from the entire source sequence is squeezed through this context vector in between the encoder & decoder.
In Bahdanau et. al 2015, Additive Attention is used to learn an alignment between all the encoder hidden states and the decoder hidden states. As the sequence is processed, the output of this alignment is used in the decoder to predict the next token.
A second type of attention is Dot-Product Attention - the alignment mechanism used in the Transformer. Instead of using addition, the Dot-Product Attention layer uses matrix multiplication to measure similarity between the query and the keys.
The dot-product acts like a similarity between the keys & values - below is a small program that plots both the dot-product and the cosine similarity for random data:
from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import cosine
data = defaultdict(list)
for _ in range(100):
a = np.random.normal(size=128)
b = np.random.normal(size=128)
data["cosine"].append(cosine(a, b))
data["dot"].append(np.dot(a, b))
plt.figure(figsize=(10, 10))
_ = plt.scatter(data["cosine"], data["dot"])
plt.xlabel("cosine")
plt.ylabel("dot-product")
Dot-Product Attention is important as it forms part of the Transformer. As you can see in the figure below, the Transformer uses multiple heads of Scaled Dot-Product Attention.
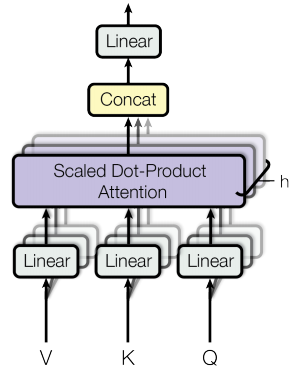
The code below demonstrates the mechanics for a single head without scaling - see Transformer Model for Language Understanding for a full implementation of a multi-head attention layer & Transformer in TensorFlow 2.
import numpy as np
import tensorflow as tf
from tensorflow.keras import Input, Model
from tensorflow.keras.layers import Dense
qry = np.random.rand(4, 16, 32).reshape(4, -1, 32).astype("float32")
key = np.random.rand(4, 32).reshape(4, 1, 32).astype("float32")
values = np.random.rand(4, 32).reshape(4, 1, 32).astype("float32")
q_in = Input(shape=(None, 32))
k_in = Input(shape=(1, 32))
v_in = Input(shape=(1, 32))
capacity = 4
q = Dense(4, activation="linear")(q_in)
k = Dense(4, activation="linear")(k_in)
v = Dense(4, activation="linear")(v_in)
score = tf.matmul(q, k, transpose_b=True)
attention = tf.nn.softmax(score, axis=-1)
output = tf.matmul(attention, v)
mdl = Model(inputs=[q_in, k_in, v_in], outputs=[score, attention, output])
sc, attn, out = mdl([qry, key, values])
print(f"query shape {qry.shape}")
print(f"score shape {sc.shape}")
print(f"attention shape {attn.shape}")
print(f"output shape {out.shape}")
# query shape (4, 16, 32)
# score shape (4, 16, 1)
# attention shape (4, 16, 1)
# output shape (4, 16, 4)This architecture also works with a different length query (now length 8 rather than 16):
qry = np.random.rand(4, 8, 32).reshape(4, -1, 32).astype("float32")
sc, attn, out = mdl([qry, key, values])
print(f"query shape {qry.shape}")
print(f"score shape {sc.shape}")
print(f"attention shape {attn.shape}")
print(f"output shape {out.shape}")
# query shape (4, 8, 32)
# score shape (4, 8, 1)
# attention shape (4, 8, 1)
# output shape (4, 8, 4)When using attention heads as shown above, hyperparameters to consider are:
Attention layers should be considered for any sequence problem. Unlike recurrent neural networks, they can be easily parallelized, making training fast. Fast training means either cheaper training, or more training for the same amount of compute.
The Transformer is a sequence model without recurrence (it doesn’t use an LSTM), allowing it to be trained without backpropagation through time.
One additional benefit of an attention layer is being able to use the alignment scores for interpretability - similar to how we can use the hidden state in an LSTM as a representation of the sequence.
This post explained four fundamental neural network layer architectures - the fully connected layer, 2D convolutional layer, LSTM layer, and attention layer.
| Layer | Intuition | Inductive Bias | When To Use |
|---|---|---|---|
| Fully connected | Allow all possible connections | None | Data without structure (tabular data) |
| 2D convolution | Recognizing spatial patterns | Local, spatial patterns | Data with spatial structure (images) |
| LSTM | Database | Sequences & memory | Never - use Attention |
| Attention | Focus on similarities | Similarity & limit information flow | Data with sequential structure |
Each layer has a different inductive bias:
For modern deep learning:
Thanks for reading!